С какой скоростью Земля движется вокруг Солнца?

Мы уже рассчитывали линейную и угловую скорости вращения Земли вокруг своей собственной оси. Давайте сегодня рассмотрим движение Земли вокруг Солнца, и найдем скорость этого движения. Ну, и заодно, рассмотрим три закона Кеплера. Куда без них.

Первый способ

С какой скоростью вращается Земля вокруг Солнца? Первое что приходит в голову, это воспользоваться уже знакомым уравнением для нахождения линейной скорости:

$\upsilon =\frac {2\pi R}{T}$

Расстояние от Земли до Солнца одна астрономическая единица или 149 597 870 700 м. Период обращения составляет один год. Если перевести это в секунды мы получим 31 536 000 с.

Подставляем это все в наше уравнение и считаем.

$\upsilon =\frac {2*3,14 *149 597 870 700}{31536000} \approx 29 790,545$ м/с

Второй способ

Но можно и пойти другим путем. Скорость движения Земли будет являться первой космической скоростью в поле тяготения Солнца. По этому, вспоминаем уравнение для нахождения первой космической скорости.

$v =\sqrt{\frac {G*M_c}{R}}$

Где G -это гравитационная постоянная, R — расстояние от Земли до Солнца, ну и M — масса самого Солнца. Остается только взвесить Солнце и произвести расчет:

$v =\sqrt{\frac {G*M_c}{R}} = \sqrt{\frac {6.67\cdot 10^{-11}\cdot 1.9985 \cdot 10^{30}}{1.496\cdot 10^{11}}}\approx 29775.559$ м/с

Часто для удобства скорость округляют и представляют как 30 км/с или 108 000 км/ч. Последний вариант, кстати, очень любят индусы. Так как в индуизме число 108 считается священным. Они даже число Пи, в свое время, определяли как отношение 339/108. Но вернемся к скорости.

Первый закон Кеплера

В наших расчетах мы принимали что Земля равномерно движется по окружности. Хотя в реальности это не совсем так.

Еще в начале XVII века немецкий астроном Иоганн Кеплер, опираясь на данные многолетних наблюдений за планетой Марс, полученные его учителем — датским астрономом Тихо Браге, заключил, что все планеты солнечной системы движутся не по окружности, а по эллипсу, в одном из фокусов которого находится Солнце. Этот закон называют первым законом Кеплера.

Все планеты Солнечной Системы движутся по эллипсу, в одном из фокусов которого находится Солнце.

Так что давайте разобраться что такое такое эллипс, и в чем его фокус.. или фокусы.

Что такое эллипс?

Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая чем расстояние между фокусами.

Рассмотрим все на простом примере. Берем шнурок с канцелярскими кнопками-гвоздиками на концах. Втыкаем кнопки в кусок гипсокартонна, который завалялся в гараже после ремонта.

Далее карандашом, опираясь на шнурок рисуем линии. Получившаяся фигура и есть эллипс, а точки куда мы втыкали кнопки называются фокусами.

Большая и малая полуось

Важными характеристиками эллипса являются его полуоси. Большая ее обычно обозначают латинской буквой «a», и малая, которую обозначают буквой «b». Тоже латинской.

Большая полуось — это расстояния от центра эллипса до самой дальней его точки. Соответственно, малая полуось — это расстояние от центра до самой ближней точки эллипса.

Эксцентриситет

Еще одна важная характеристика эллипса носит шикарное название — эксцентриситет. Его обычно обозначают буквой «е» и определяют как отношение фокусного расстояния эллипса (c) к большой полуоси (a).

$e =\frac {c}{a}$

Эллипс иногда называют сплющенной окружностью. Так вот эксцентриситет как раз показывает насколько эта окружность сплющена.

Для эллипса:

$0<e<1$

Чем ближе эксцентриситет к единице, тем более вытянутый эллипс мы получим. И наоборот эксцентриситет близкий к 0, будет иметь эллипс ну очень похожий на окружность. В принципе можно сказать что окружность это эллипс с е=0.

В солнечной системе самый маленький эксцентриситет у Венеры всего 0,007, то есть траектория ее движения это практически окружность. Эксцентриситет близкий к единице имеют кометы. К примеру у кометы Галея е=0,967.

Что же касается Земли, то эксцентриситет земной орбиты тоже очень близок к нулю, всего 0,017. Но тем не менее это не ноль. А это значит что расстояние от Земли до Солнца величина отнюдь не постоянная.

Афелий и перигелий

Точка в которой планета находится ближе всего к Солнцу называется перигелий. От греческого perihelion, “peri“ — рядом и “helios“ — Солнце. Противоположная перигелию точка называется афелий. Соответственно это точка где планета максимально удалена от светила.

Земля находится перигелии, начале января. Она приближается к Солнцу на расстояние в 147,1 миллионов километров. Афелий она проходит в начале июля, когда удаляется на 152,1 миллионов километров. Разница выходит около 5 миллионов километров.

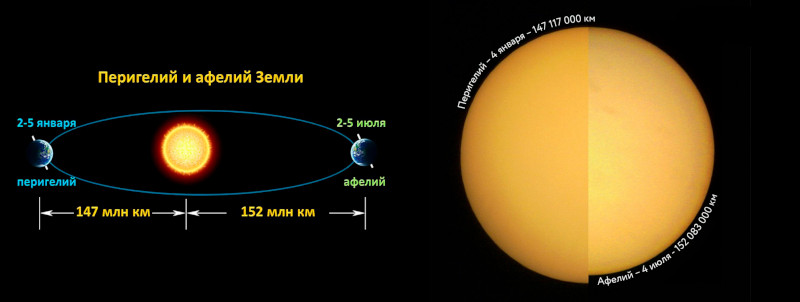
Этим иногда объясняют то что зимы в северном полушарии менее суровые, нежели в южном. Все таки зимой мы чуть ближе к солнцу. С другой стороны так как земля получает меньше солнечной энергии в июле, лето в северном полушарии более прохладное.

Второй закон Кеплера

Итак, мы сказали что согласно первому закону Кеплера Земля движется не по круговой, а по эллиптической орбите. Что же касается ее скорости, то она возрастает при приближении к Солнцу, и убывает при удалении от него.

Кеплер сформулировал это следующим образом:

За одинаковые промежутки времени радиус-вектор планеты описывает одинаковые площади.

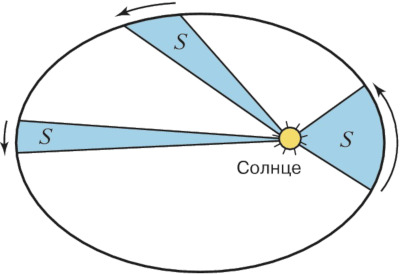
Это так называемый закон площадей или второй закон Кеплера, пожалуй в самой бесполезной его формулировке. Но фактически мы имеем дело с законом сохранения момента импульса. И куда больший интерес для нас будет иметь следующее уравнение:

$\upsilon_1\cdot r_1 =\upsilon_2\cdot r_2$

Произведение линейной скорости и радиус-вектора в перигелии, равно произведению скорости и радиус-вектора афелии. Это частный случай второго закона Кеплера, соответственно для максимального и минимального значений скорости движения планеты.

Максимальная и минимальная скорость движения Земли

Зная это можно, рассчитать с какими скоростями движется Земля перигелии и афелии. То есть найти ее максимальную и минимальную скорости. Но здесь нам понадобится закон сохранения энергии.

$\frac {m\upsilon_1^2}{2} - G \frac { M_c \cdot m}{r_1} = \frac {m\upsilon_2^2}{2} - G \frac {M_c \cdot m}{r_2}$

А так же, формулы для определения расстояний от солнца до афелия и перигелия, через эксцентриситет и большую полуось:

$r_1 = a(1-e)$

$r_2 = a(1+e)$

Ну и пожалуй уравнение для нахождения первой космической скорости.

$\upsilon =\sqrt{\frac {G*M_c}{R}}$

Единственное в формуле расстояние R мы заменим на a, то есть на большую полуось. Большая полуось земной орбиты — это среднее расстояние от Земли до Солнца, и именно значение большой полуоси мы использовали в расчетах в самом начале. А значит скорость которую мы рассчитывали в самом начале есть средняя орбитальная. Она нам пригодится.

$\upsilon =\sqrt{\frac {G*M_c}{a}}$

Составляем небольшую систему уравнения и с точки зрения физики задача решена. Остается только математика.

$\begin{cases} \upsilon_1\cdot r_1 =\upsilon_2\cdot r_2\\ \frac {m\upsilon_1^2}{2} - G \frac { M_c \cdot m}{r_1} = \frac {m\upsilon_2^2}{2} - G \frac {M_c \cdot m}{r_2}\\ r_1 = a(1-e)\\ r_2 = a(1+e)\\ \upsilon =\sqrt{\frac {G*M_c}{a}} \end{cases}$

Начнем с того, что сократим массу Земли в законе сохранения энергии, а так же заменим радиус векторы $r_1, r_2$ на, соответственно, $a(1-e)$ , $a(1+e)$ .

$\begin{cases} \upsilon_1\cdot a(1-e) =\upsilon_2\cdot a(1+e)\\ \frac {\upsilon_1^2}{2} - G \frac { M_c}{a(1-e)} = \frac {\upsilon_2^2}{2} - G \frac {M_c}{a(1+e)}\\ \upsilon =\sqrt{\frac {G*M_c}{a}} \end{cases}$

Если внимательно посмотреть, то можно увидеть что в отношениях $G \frac { M_c}{a(1-e)}$ , и $G \frac {M_c}{a(1+e)}$ , $G \frac {M_c}{a}$ , это квадрат средней орбитальной скорости $\upsilon ^2$ . А ее мы уже рассчитали в самом начале. Так что здесь удобно будет выполнить замену.

$\begin{cases} \upsilon_1\cdot a(1-e) =\upsilon_2\cdot a(1+e)\\ \frac {\upsilon_1^2}{2} - \frac { \upsilon ^2}{1-e} = \frac {\upsilon_2^2}{2} - G \frac {\upsilon ^2}{1+e}$

Теперь из первого уравнения выражаем $\upsilon_2$ , и подставляем это все во второе. Делаем все необходимые преобразования и выражаем $\upsilon_1$ :

$\upsilon_1 =\upsilon \sqrt{\frac {1+e}{1-e}}$

Ну и теперь так же выражаем $\upsilon_2$ :

$\upsilon_2 =\upsilon \sqrt{\frac {1-e}{1+e}}$

Остается только подставить значения, и посчитать.

$\upsilon_1 = 29775.559 \sqrt{\frac {1+0.017}{1-0.017}} \approx 30 286,1$ м/с

$\upsilon_2 = 29775.559 \sqrt{\frac {1-0.017}{1+0.017}} \approx 29 273,6$ м/с

Третий закон Кеплера

Опубликовав в 1609 г. два своих закона Иоганн Кеплер так и не остался удовлетворен, и продолжил поиски, которые спустя десять лет привели его к открытию третьего закона.

Квадраты звездных периодов обращений планет относятся между собой как кубы больших полуосей их орбит.

$\frac {T_1^2}{T_2^2}} =\frac {a_1^3}{a_2^3}}$