Как найти площадь круга? У меня этот вопрос встал очень остро на экзамене по физике в университете, когда я решал одну из задач. Память человека вещь непредсказуемая, сегодня ты помнишь все до мелочей, а завтра это все уже выветрилось из головы. И благо если это была глупость какая, а если нет? Если это день рождения жены или тещи, пароль аккаунта в контакте, или площадь круга. Как это было в моем случае.
Здравствуйте дорогие друзья, меня зовут Валентин Анатольевич, и сегодня мы вычисляем площадь круга 3 способами. Точнее способ будет один, это формула ![]() , но вот варианты ее получения будут различны.
, но вот варианты ее получения будут различны.
Честно говоря, я уже и не помню правильно или нет решил ту задачу, я даже не помню, что это была за задача. Но сам момент того, как выполняя промежуточные расчеты я интегрировал уравнение окружности, чтоб получить казалось бы, простейшую формулу из школьной программы… сильно врезался в память
Итак, первый способ у нас будет от студентов физико-математических факультетов.
Интегрирование.
1. Берем уравнение окружности. Для тех, кто не знает его легко получить из теоремы Пифагора, заменив там катеты на координаты x и y, а за гипотенузу приняв радиус R. Конечно, при условии, что центр окружности будет находится на пересечении координатных осей.
![]()
К счастью, это я помнил.
2. Выражаем y.
![]()
3. Если вычислить определенный интеграл для значений x от 0 до R, мы получим площадь одной четверти круга.
![Rendered by QuickLaTeX.com \[\frac{1}{4}S=\int\limits_0^R \sqrt{R^2-x^2}\,dx\]](https://newtonov.ru/wp-content/ql-cache/quicklatex.com-7479e3008654e9c55630ae7d0c7ce5ec_l3.png)
Соответственно, чтоб получить всю площадь, нам необходимо будет все это безобразие до множить на 4.
![Rendered by QuickLaTeX.com \[S=4\int\limits_0^R \sqrt{R^2-x^2}\,dx\]](https://newtonov.ru/wp-content/ql-cache/quicklatex.com-2b4a6b16249e47f6a9dfc672448a89a6_l3.png)
4. Давайте выполним замену переменной, и представим x как ![]() . Тогда:
. Тогда: ![]() .
.
5. Найдем пределы интегрирования. Для этого необходимо в наше уравнение замены переменной подставить значения x и вычислить чему будет равно t при этих значениях. Получаем промежуток от 0 до ![]() .
.
6. Итак запишем нашу формулу:
![Rendered by QuickLaTeX.com \[S=4\int\limits_0^{\frac{\pi}{2}} \sqrt{R^2-R^2\sin^2t}\,R \cos tdt\]](https://newtonov.ru/wp-content/ql-cache/quicklatex.com-704a72c6e8263e0685fa3df05b5b1ac2_l3.png)
7. Сделаем еще кое какие математические преобразования и вычислим определенный интеграл по формуле Ньютона -Лейбница.
![]()
![Rendered by QuickLaTeX.com \[S=4R^2\int\limits_0^{\frac{\pi}{2}} cos^2t dt = 4R^2\int\limits_0^{\frac{\pi}{2}} \frac{1}{2}}(1+ 2cos{2t}) dt = 2R^2(\int\limits_0^{\frac{\pi}{2}} dt + \int\limits_0^{\frac{\pi}{2}} \cos 2t dt) =\]](https://newtonov.ru/wp-content/ql-cache/quicklatex.com-28adf484dcf6d0491f78ba9e93b79cf4_l3.png)
![]()
Готово!!! В принципе, не так сложно если не впадать в ступор при виде синусов и косинусов, а также уметь интегрировать.
Но вот вопрос. Люди умели находить с большой точностью площадь круга и до интегрального исчисления. Поэтому давайте попробуем обойтись интегралов.
Площадь прямоугольника
Условно, можно сказать, что площадь — это количество квадратиков, со стороной в единицу помещающихся в данной фигуре. К примеру, кухня в хрущевке имеет размеры 2 на 3 метра. Перемножаем длину на ширину и получаем площадь 6 квадратных метров. То есть если у нас имеется 6 квадратных кусков линолеума, со стороной в 1 метр, мы ими полностью без остатка, покроем весь пол.
Прямоугольную кухню легко разбить на квадраты, но что делать если у нас круг? Скажем круглый кусок сыра.
Любой старший прапорщик, обладая не дюжей армейской смекалкой вам скажет, что нужно в таком случае из круга сделать прямоугольник. И он окажется прав. Почему? По тому что старший прапорщик всегда прав.
В общем метод номер два. Метод старших прапорщиков.
Перегруппировка
Делим круг на восемь равных секторов и совмещаем друг с другом.
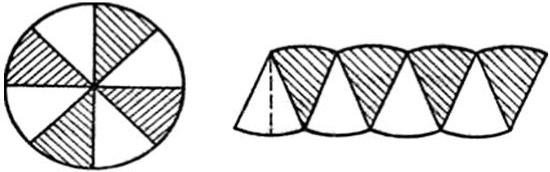
Отдаленно напоминает прямоугольник? Нет? Отжимаемся восемь раз, и делим еще.

Если секторов будет бесконечно много, то в таком случае, искривления их дуг будут незначительны. А это значит мы получим уже треугольники.
Опять совместим их друг с другом как и в первом случае. И у нас уже идеальный прямоугольник, с шириной равной радиусу ![]() , и длиной в половину длины окружности, то есть
, и длиной в половину длины окружности, то есть ![]() .
.
Перемножаем получаем:
![]()
Если внимательно посмотреть на полученную формулу мы увидим, что с её помощью можно найти площадь прямоугольного треугольника с основанием равным длине окружности и высотой равной ее радиусу.
Равенство площадей такого треугольника и круга доказывал Архимед, в своей работе о площадях круга.
Я не буду приводить здесь доказательство этой теоремы, скажу только, что Архимед использовал многоугольники. Один вписанный в окружность, а другой описанный вокруг нее. Площадь круга находилась где-то между площадями этих многоугольников, причем при увеличении сторон, их площади приближались друг к другу, а значит приближались и к площади круга.
Но все же как получить из круга треугольник? Давайте воспользуемся методом неделимых Бонавентуры Кавальери.
Метод неделимых
Представим, что наш круг состоит из бесконечно большого числа окружностей, толщина линий которых стремится к нулю. Если развернуть эти окружности в отрезки и сложить друг на друга стопкой, мы получим треугольник с основанием равным длине большей окружности, то есть ![]() и высотой равной радиусу.
и высотой равной радиусу.
Площадь треугольника как известно это половина произведения основания на высоту.
Или в нашем случае ![]() .
.

Те, кто внимательно слушал, наверно помнят, что в теореме Архимеда говорится о прямоугольном треугольнике. Но его довольно легко получить сместив наши отрезки к левому или правому краю. К слову, так легким движением мы докажем еще одну теорему из школьной геометрии. Если знаете какую, пишите в комментариях.
Так же можете написать, как старшие прапорщики находят объем шара, или как бы с этой задачей справился Бонавентура Кавальери.
А я с вами прощаюсь, желаю счастья и до скорых встреч.


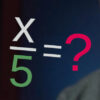






Стереотипы влияют на ход мысли. Поэтому для получения формулы площади круга использовались вписанные и описанные многоугольники, деление на множество одинаковых секторов. Только Архимед сравнил площадь круга с площадью прямоугольного треугольника, правда, это могла быть только аналогия, потому что никаких доказательств он не привёл (может, просто мне не удалось найти). Могу доказать (найти) формулу площади круга с помощью прямоугольников за один, максимум, два шага
Буду рад видеть доказательство в комментариях ниже))
Древние философы и математики не знали дифференциального и интегрального исчисления, пользовались ограниченным набором инструментов. Как бы действовал я, будь на их месте. Круг — колесо, а колесо должно двигаться…
К сожалению в поле комментария невозможно вставить файлы, иллюстрирующие доказательство, а это может затруднить понимание. Предлагаю написать мне на мой Email, чтобы я смог ответить. Сочтёте достойным внимания — выложите для общего обозрения с опровержениями, замечаниями и т.д.
День добрый, Валентин Анатольевич.
Я не смог (технически) у вас в комментариях изложить свою версию или отправить вам полный вариант, однако, у Вас есть возможность ознакомиться с моими рассуждениями в комментариях на сайте: https://zen.yandex.ru/media/tehno_chtivo/kak-drevnie-uchenye-nashli-ploscad-kruga-5e7a460e18ca9e1754516625?comment-request=1#comment_1080357914
С уважением, Алексеев Сергей